
Photo by Conny Schneider on Unsplash
Build a Neural Network from Scratch in Just 10 Minutes
Fast and Simple Instructions for building Neural Network
Trying to dip your toes into Deep Learning? Wondering how those PyTorch and TensorFlow neural networks work behind the scene? What better way than to build one yourself? We will be using just numpy and some trivial maths (okay not that trivial, but let's just go ahead).
Prerequisites:
- Partial Derivatives: Since we have to differentiate things to find the minima, we will have to use partial derivatives. But don't worry, the only thing you need to know is the chain rule of partial differentiation, which goes like this (given that z is a function of two variables x and y, and both x and y depend on a common variable s):
$$∂z/∂s = (∂z/∂x)(∂x/∂s) + (∂z/∂y)(∂y/∂s)$$
Neurons and Neural Networks: Though we will discuss these briefly, our main focus will be on the implementation of neural networks and backpropagation. (If you want to review them again, try this video).
Transpose and Dot Product: Not much to learn there.
Numpy: Obviously, duh.
Neuron and Networks:
So neural networks are made up of neurons, which is the tiniest unit of the network which works like a switch:
The neuron (imagine it like a box) receives different types of input from various sources.
It adds them up and sends them to an activation function.
If the output of this activation function is greater than the decided threshold, then the neuron will fire. Boom.
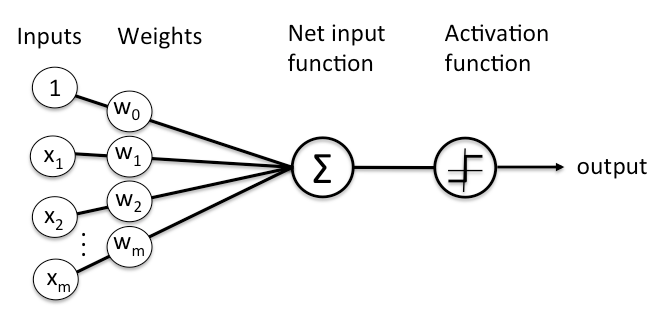
A neural network, therefore, contains a number of such neurons (obviously). But they are arranged in layers. A neural network has at least three layers :
Input Layer: It contains neurons corresponding to the sources of input.
Hidden Layer: You can have more than one hidden layer and can have any number of neurons in each layer. That is something which we can optimize later by trail and error.
Output Layer: It contains the number of neurons corresponding to the number of output classes you want (only one in regression case).
You might question what these weights are. Well, each connection between a neuron of two layers has a weight associated with it, and each neuron has a certain bias.
These are used to calculate the output according to the formula (where x is the input value):
$$z = wx + b$$
Weights help to guide the network based on the significance of the input. We can assign a larger weight to more important neurons and negative weights to others. Bias helps to adjust the threshold of that particular neuron.

Image source: Reddit Preview
This means that bias is specific to a particular neuron, or we can say, a layer will have its own set of biases. While the connections between two layers will have their own set of weights. Based on this, let's write some code to define the structure of our neural network.
import numpy as np
import matplotlib.pyplot as plt
class NeuralNetwork:
def __init__(self, input_layer_size, hidden_layer_size, output_layer_size, learning_rate = 0.01):
self.weights_input_to_hidden = np.random.rand(input_layer_size, hidden_layer_size)
self.hidden_layer_bias = np.random.rand(hidden_layer_size)
self.weights_hidden_to_output = np.random.rand(hidden_layer_size, output_layer_size)
self.output_layer_bias = np.random.rand(output_layer_size)
self.learning_rate = learning_rate
Activation Function:
The summation of all the inputs is put into an activation function which generates the output between some range (say sigmoid) :
$$σ(x)= 1/(1+e^{-x}) $$
What’s this bogus-looking term? Why do we even need an activation function at the first place? Short answer, we will be just repeating the Linear Regression process in a much more convoluted way and nothing else. To understand the maths behind this, you can watch this video on activation functions. But the crux is, that we need a non-linear activation function like sigmoid or ReLU() for our contraption to work.
Therefore, the actual output of our neuron is σ(z), where z = wx + b.
Now what else than to code our activation function (and it’s derivative) as well? (You can define them inside or outside of the class)
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(x):
return x*(1-x)
Forward Propagation:
Remember how the neural network worked? We do a dot product of the input layer with the weight vector corresponding to the input-hidden layer. Then, we add the hidden layer’s bias to product to obtain z vector. Then pass it in the activation function to give the output. This part is actually simple to code despite of how it looks.
def forward(self, X):
self.hidden_input = np.dot(X, self.weights_input_to_hidden) + self.hidden_layer_bias
self.hidden_output = sigmoid(self.hidden_input)
self.final_input = np.dot(self.hidden_output, self.weights_hidden_to_output) + self.output_layer_bias
self.final_output = sigmoid(self.final_input)
return self.final_output
Optimization and Gradient Descent:
Before we understand this, it is essential to first define our loss function. It is a way to measure the performance of our network, by representing how wrong it is compared to the true value in numbers. One of the way to do that is to use the Mean Squared error.
def mse_loss(y_true, y_pred):
return np.mean((y_true - y_pred) ** 2)
You might remember from your calculus class, that we can equate the derivative of a function to zero to find its maxima/minima. So if we do the same for our loss function, we can actually find the right parameters to minimize the loss.
Only that the computer cannot perform differentiation in the same way as we do. Therefore, we use another technique called Gradient Descent.
The intuition behind gradient descent is fairly straightforward: imagine you're on a hilly landscape, and your goal is to find the lowest point in that landscape (which represents the minimum loss or error in a neural network). What would you do?
Find the steepest slope in all directions.
Go towards that.
Repeat.
Fairly simple, as said before. The step size is decided by the learning rate which we have included in the structure beforehand (missed it? haha, got you). All we need to code the part where:
Compute the gradient at each point w.r.t the parameter (weights and biases).
The model's parameters are then adjusted in the opposite direction of the gradient to reduce the loss. The size of the adjustment is controlled by a value called the learning rate α.
$$\text{parameter}_{\text{new}} = \text{parameter}_{\text{old}} - \alpha \cdot \nabla \text{Loss}$$
where ∇Loss represents the gradient of the loss function with respect to the parameter.
Back Propagation:
The idea behind back propagation is that it is easier to go backwards because we can store the partial derivatives of the loss function with respect to initial layers while calculating. We can then reuse some of them as they will be required when calculating partial derivatives of the loss function with respect to initial layers according to the chain rule.
Confusing? It is better to see some action rather than rely on convoluted terminology. Let’s see a backward pass in action.
Remember our MSE loss function?
$$L = \frac{1}{2}(y-\hat{y})^2$$
where y is true output and y^ is predicted output. Its derivative w.r.t predicted output will look like:
$$\frac{\partial L}{\partial \hat{y}} = \hat{y} - y$$
And we know that :
$$\hat{y} = \sigma(z_2)$$
Next, we compute the gradient of the loss with respect to the input to the output layer (say z2):
$$\frac{∂L}{∂z_2} = \frac{∂L}{∂\hat{y}}⋅\frac{∂\hat{y}}{∂z_2}$$
where we already know the first and second term (the second term is just derivative of sigmoid function which we have defined beforehand).
Therefore,
$$\frac{\partial L}{\partial z_2} = (\hat {y}−y)⋅y^⋅(1−\hat{y})$$
Now we know that:
$$\begin{align} z_2 &= W_2h+B_2, \\ \\ h &= \sigma(z_1) \qquad and, \\ \\ z_1 &= W_1x+B_1 \end{align}$$
So if we try to find the derivatives of the loss function w.r.t weights between the hidden and output layer (W2) and biases of the output (b2) in a similar fashion then they will be:
$$\begin{align} \frac{\partial L}{W_2} &= \frac{\partial L}{\partial z_2}.\frac{\partial z_2}{\partial W_2}\space\space\space \text {and,}\\ \\ \frac{\partial L}{\partial B_2} &= \frac{\partial L}{\partial z_2}.\frac{\partial z_2}{\partial B_2} \end{align}$$
which is :
$$\begin{align} \frac{\partial L}{W_2} &= \frac{\partial L}{\partial z_2}.h \space\space\space \text {and,}\\ \\ \frac{\partial L}{\partial B_2} &= \frac{\partial L}{\partial z_2} \end{align}$$
Now time to cover this math in a beautiful veil of code just like everything else in Machine Learning.
def backward(self , X, y, output):
loss_gradient = 2 * (output - y) / y.size
del_output = loss_gradient*sigmoid_derivative(output)
d_weights_hidden_output = np.dot(self.hidden_output.T, del_output)
d_bias_output = np.sum(del_output, axis = 0)
similarly for the next layer:
$$\begin{align} \frac{\partial L}{\partial z_1} &= \frac{\partial L}{\partial z_2}.\frac{\partial z_2}{\partial z_1} \\ \\ &= \frac{\partial L}{\partial z_2}.\frac{\partial z_2}{\partial h}.\frac{\partial h}{\partial z_1} \\ \\ &= \frac{\partial L}{\partial z_2}.{W_2^T}.{\sigma'(z_1)} \end{align}$$
and for the parameters:
$$\begin{align} \frac{\partial L}{W_1} &= \frac{\partial L}{\partial z_1}.h \space\space\space \text {and,}\\ \\ \frac{\partial L}{\partial B_1} &= \frac{\partial L}{\partial z_1} \end{align}$$
Coding it up as well (continued in the same backwards function):
del_hidden = np.dot(del_output, self.weights_hidden_to_output.T)*sigmoid_derivative(self.hidden_output)
d_weights_input_hidden = np.dot(X.T, del_hidden)
d_bias_hidden = np.sum(del_hidden, axis=0)
adding the equations of gradient descent which we have discussed before:
self.weights_hidden_to_output -= self.learning_rate * d_weights_hidden_output
self.output_layer_bias -= self.learning_rate * d_bias_output
self.weights_input_to_hidden -= self.learning_rate * d_weights_input_hidden
self.hidden_layer_bias -= self.learning_rate * d_bias_hidden
Yayy. Our Neural network is almost complete, except for some formalities.
Training function:
Now we also need to write a train function which will utilize these forward and backward functions to train our neural network.
def train(self, X, y, epochs):
for epoch in range(epochs):
output = self.forward(X)
self.backward(X, y, output)
loss = mse_loss(y, output)
if epoch % 1000 == 0:
print(f"Epoch {epoch} Loss: {loss}")
Testing on Xor data:
You can use some other dataset as well. For this one, the input array will be of size (4,2). And the result should be close to [0, 1, 1, 0].
X = np.array([[0, 0],
[0, 1],
[1, 0],
[1, 1]])
y = np.array([[0], [1], [1], [0]])
# Initialize Neural Network
nn = NeuralNetwork(input_layer_size=2, hidden_layer_size=5, output_layer_size=1, learning_rate=0.1)
nn.train(X, y, epochs=10050)
output = nn.forward(X)
print("Predicted Output:")
print(output)
Conclusion:
Our neural network is complete now. If you still want some exercise for your brain, try to figure out why we have used Transpose in these lines in the backward function and not in forward function.
d_weights_hidden_output = np.dot(self.hidden_output.T, del_output)
d_weights_input_hidden = np.dot(X.T, del_hidden)
Or if you want to code something as well, try optimizing the result further on your own.
Reference:
Some youtube videos which helped me a lot and might help you as well:
